Вот и закончился у меня замечательный предмет “Специальные главы высшей математики”, основной его частью были уравнения математической физики. Пока ещё не всё забылось, хотелось бы пощупать их на практике. Скорее всего я ещё не раз столкнусь в своей жизни с нуждой решить урчапы, но это по любому будет какая-нибудь физика неосязаемого и непредставимого, а хочется ведь увидеть эти уравнения в действии.

Статья вышла странной по содержанию, потому что изначально я как всегда планировал сделать чуть-чуть, поведать тем, кто живёт в счастливом неведение, о великолепии пространств, но меня повело не туда. Я думаю, первая часть статьи будет не так интересна тем, кто разбирается более или менее, поэтому можете сразу прыгнуть сюда, ну или если вам ну очень это всё не интересно, можете тоже туда прыгать, там прикольные картинки и видео.

Взаимоотношения в пространствах

Конечно разные уравнения это очень интересно, но мне больше запомнились пространства, скорее всего потому что им было уделено пол-лекции, поскольку мы их “вспоминали”, я лично впервые узнавал… Я помнил что-то про метрические пространства, потому что на зачёте про них был вопрос, но не более. В общем для меня они сохранили шарм чего-то неизведанного.

Ну ладно пора заканчивать вступление, так что же такое пространство? В математике, как обычно взяли всем привычную вещь, ободрали и оставили только нужное, так вот пространство это объекты и отношения между ними, лаконичнее не скажешь. Вокруг вас наверное сейчас мебель (извиняюсь перед теми кто в лесу, придумайте что-то сами), но она не просто существует, она как-то расположена относительно других объектов. Таким вот образом мы подбираемся к первому взаимоотношению — метрике, ну или по простому расстоянию. У кого-то сразу в голове наверное возникла теорема Пифагора. Естественно не одной этой функцией едины, далеко за примерами ходить не надо, можно просто голову поднять. Самолёты летают на достаточно большие расстояния, чтобы ощутить кривизну земли, для них кратчайший путь не прямая линия, значит и теорема Пифагора для них работать будет не так хорошо. Получается расстояние это набор функций, но не может же это быть любая функция, всё таки у нас есть какие-то ожидания, например, расстояние должно быть положительным. Собственно оно так и есть, у метрики есть набор ограничений:

1. Если между объектами расстояние равно нулю, то это один и тот же объект (\(\rho(x,y)=0 \Leftrightarrow x=y\))
2. От куда бы мы не начинали измерять, расстояние остаётся одинаковым (\(\rho(x,y)=\rho(y,x)\))
3. Метрика определяет кратчайшую длину пути между двумя точками (\(\rho(x,y) \leq \rho(x,z)+\rho(z,y)\))
4. Ну и как мы уже говорили, расстояние не должно быть отрицательным (\(\rho(x,y) \geq 0\))

Положение мы определили, а что насчёт габаритов. Тут напрягаться не надо чтобы придумать 100 способов измерить размеры: длины, объёмы, площади и так далее. За это отвечает норма. Сложно будет, даже скорее неправильно, продолжать аналогию с мебелью, потому что норма по хорошему задаётся на линейном пространстве, хотя кто сказал что мы не можем определить пространство шкафов, главное чтобы мы могли их складывать между собой и умножать на скаляр, но для интуитивности перейдём на пути. Чего мы ждём от размеров, конкретнее — длины пути:

1. Естественно длина не должна быть отрицательной (\(||x|| \geq 0\))
2. Пройти три метра это тоже самое, что пройти три раза метр (\(||\alpha x||=|\alpha|\cdot||x||\))
3. Норма двух путей меньше или равна сумме длин этих путей по отдельности. И поэтому мы перешли на пути: думаю, всем понятно, что если сделать 2 шага вперёд и один назад, то всего будет 3 шага, а общий путь будет равен 1 шагу. Хотя если взять габариты стульев, как коробку в которую их можно поместить, то возможно представить такое расположение в котором их общие размеры меньше, чем по отдельности (\(||x+y||\leq||x||+||y||\))
4. Для разных объектов размеры могут совпадать, но при этом мы точно знаем, что только для нулевого вектора длина равна нулю. Тут я решил обойтись без сравнений, потому что ноль в целом это особая штука, которая описывает отсутствие чего-то, то есть нельзя сказать, что нет объекта с габаритами равными нулю, потому что он есть и у него имеются уникальные свойства, но при этом он как бы описывает отсутствие объекта (\(||x|| = 0 \Leftrightarrow x=0\))

Да уж, мы приближаемся к чему-то странному, если на описание, как кажется, интуитивно понятных вещей уходят целые абзацы. Я долго думал какое подобрать сравнение, но скалярное произведение это скалярное произведение, операция с удобными свойствами, поэтому просто опишу какие к ней есть требования:

1. \((x,x)\geq 0\)
2. \((x,x)=0 \Leftrightarrow x=0\)
3. \((x,y)=(y,x)\)
4. \((x+y,z)=(x,z)+(y,z)\)
5. \((\alpha x,y)=\alpha(x,y)\)

Через скалярное произведение можно задать норму и метрику, например:

\[ \rho(x,y)=||x-y||=\sqrt{(x-y,x-y)} \]

До чего доводит обобщение

Подготовка закончена, мы ввели всё необходимое, чтобы начать наше исследование неизведанного!!!

Собственно основной магией всего этого, для меня, является обобщение. Я конечно приводил примеры, но не определял иксы и игреки, вообще они тоже имеют ограничения, но углубляться не будем, иначе так можно закопаться до ядра Земли, главное чтобы их можно было складывать и умножать на что-то.

Давайте тогда создадим собственное пространство \(I\), итальянских животных (ну или изображений, если вы леймчик 🙄). Их нужно как-то формализовать, в общем случае это прямоугольник из разноцветных точек. Возьмём не прямоугольник, а единичный квадрат, так будет проще для расчётов, перед обработкой сжимаем или обрезаем, а после разжимаем, если то нужно. Цвета можно представить разными способами: RGB, RGBA, HSL, просто L — в целом это какой-то набор чисел, причём они ограниченны, чаще всего от 0 до 255, иногда от 0 до 1, опять же возьмём второй вариант для простоты. Вообще мы должны использовать векторы для этих задач, в хорошем цветовом пространстве расстояния очень точно передают то, что воспринимает человек, однако я решил сделать проще и рассматривал многоканальные изображения, как несколько одноканальных, а потом склеивал их вместе. Сильно ли это влияет на финальный результат? Количественно — скорее всего да, качественно — не должно.

Получилось неплохое множество функций, но до пространства немного не хватает. Обычно для функций задают скалярное произведение через интеграл от произведения функций, но сейчас не все элементы интегрируемы. Реальные изображения в основном состоят из плавных переходов, поэтому вполне приемлемо потребовать, чтобы наши функции были кусочно-непрерывными, причём мы точно знаем, что число отрезков, где функция непрерывна, конечно. Возможно это избыточно, но достаточно хорошо описывает реальность, и открывает большой простор, в частности оказывается, что \(I\) это подпространство хорошо изученного пространства \(L^{2}\) — пространства функций, чьи квадраты можно проинтегрировать по Лебегу, благо в нашем случае интеграл Лебега будет совпадать с интегралом по Риману.

Давайте посмотрим, что у нас получилось: вот кусочек нашего пространства в виде графа, где длины рёбер пропорциональны расстояниям между точками.

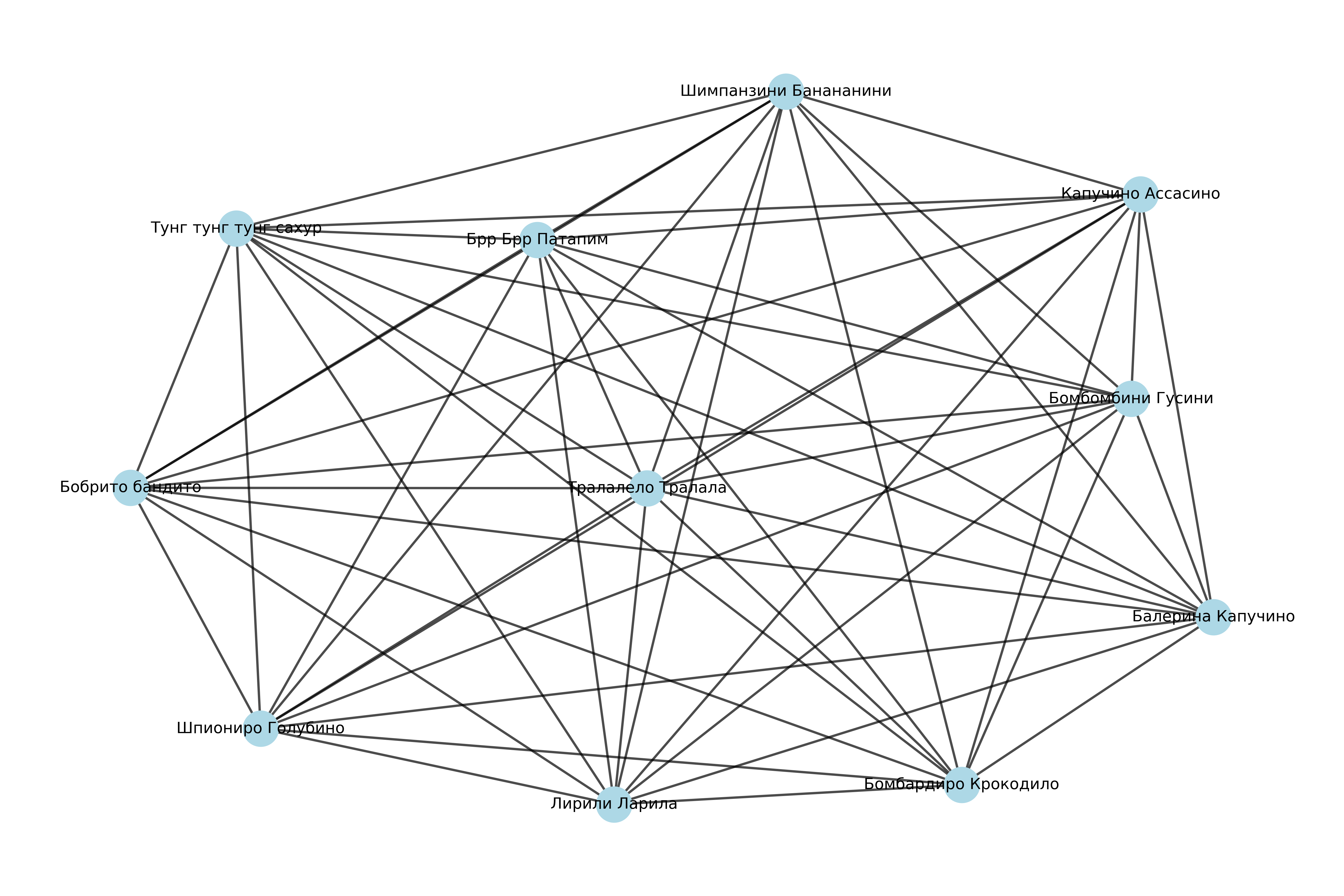
Репрезентативность не самая хорошая, но что-то в этом есть. Бомбини Гусини достаточно близко к Бомбардиро Крокодило, но при этом Капучино Ассасино оказался ближе к нему, предполагаю, потому что у Бомбини Гусини на фоне тучи и это перекликается с ночью на изображении Капучино Ассасино. Так же это объясняет почему Тралело Тралала на таком же расстоянии от Бомбардиро Крокодило, как Бомбини Гусини, ясное небо у Бомбардиро Крокодило сильно совпадает с таковым у Тралело Тралала.

Задача Шипанзини-Лирили

Мы посмотрели на известные нам островки, а что находится между ними? По большей части всякий шум, но и все известные нам изображения, этакая вавилонская библиотека. Если мы будем просто случайно выбирать места, то понятное дело по большей части будет попадаться какой-то мусор, поэтому давайте отправимся в мореплавание от Шимпанзини Бананини к Лирили Ларила.

Зададим наш маршрут некой функцией \(u(x,y,t)\), где \(t\) изменяется от 0 до 1, соответственно при \(t=0\) у нас первая картинка, при \(t=1\) вторая. Плыть просто по прямой не так интересно, поэтому скажем, что путь подчиняется какому-то закону, например, \(u_{tt} -\Delta u = 0\).

\[ \begin{cases} u_{tt}-\Delta u = 0 \\ u|_{t=0}=I_{1}(x,y) \\ u|_{t=1}=I_{2}(x,y) \end{cases} \]

Я захотел воспользоваться методом Галёркина для нахождения нашего маршрута, уж очень мне он нравится, а в жизни случаев просто так использовать его мне не выпадало, наверное, и к лучшему. Первое, что нужно сделать, — это выбрать набор функций, обзовём их \(V_{s_{x}s_{y}}(x,y)\), но вообще отложим их в сторону и будем решать в общем виде, по нужде наложим ограничения и из оставшегося выберем то, что лучше подойдёт. Решение у нас приближённое, поэтому будем использовать не \(u\), а \(W_m\), где \(m\) это порядок приближения. Ну и представим решение как разложение по \(V_{s_{x}s_{y}}\).

\[ W_{m}=\sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C_{s_{x}s_{y}}(t)V_{s_{x}s_{y}}(x,y) \]

Подставим это в исходное уравнение и получим следующую пакость:

\[ \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C''_{s_{x}s_{y}}(t)V_{s_{x}s_{y}}(x,y) = \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C_{s_{x}s_{y}}(t)\Delta V_{s_{x}s_{y}}(x,y) \]

Некая мерзость, вы мне можете не верить, но мы облегчим себе жизнь если возьмём от этого скалярное произведение в пространстве итальянских животных.

\[ \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C''_{s_{x}s_{y}}(t) \left(V_{s_{x}s_{y}}(x,y),V_{k_{x}k_{y}}(x,y)\right)_I = \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C_{s_{x}s_{y}}(t) \left(\Delta V_{s_{x}s_{y}}(x,y),V_{k_{x}k_{y}}(x,y)\right)_I \]

Настало время накладывать ограничения. Первое, что я хочу, — это чтобы базис из выбранных функций был ортонормированным в \(I\), тогда слева скалярное произведение уйдёт и заодно заберёт с собой суммы. А вот справа дела посложнее, потому что не понятно, чо такое \(\Delta V_{s_{x}s_{y}}\). Не сложными манипуляциями можно доказать, что перед нами скалярное произведение просто двух функций в \(H_{1}^{0}\) (пространстве Соболева) — пространство финитных функций из \(L^{2}\), у которых есть обобщённая производная. Становится чуть понятнее, но неприятнее, добиться ортонормированности везде не выйдет, ну у меня по крайней мере не получилось, но мы можем добиться ортогональности, что уже хорошо. Если мы скажем, что \(\Delta V_{s_{x}s_{y}} = \lambda_{s_{x}s_{y}}V_{s_{x}s_{y}}\), то бишь собственной функцией оператора Лапласа, то мы сможем вынести константу из скалярного произведения. Погодите… Собственные функции оператора Лапласа…

Мне некуда деться от метода Фурье. Не подумайте, метод замечательный, но это не так интересно. И да, в целом никто не запрещает просто убрать эти ограничения и взять случайный базис, но у меня присутствует проблема с навыком решения системы диффуров и разбираться с гадостями, которые получатся без них, я не хочу. В общем не буду даже выводить, просто скажу, что наши функции имеют следующий вид:

\[ V_{s_{x}s_{y}}(x,y)=2\sin(s_{x}\pi x)\sin(s_{y}\pi y) \]

Ещё из \(H_{1}^{0}\) следовало, что функции должны быть финитными, но тут лучше заметно, что аппроксимированное изображение будет иметь чёрную виньетку, с увеличением приближения она должна становиться меньше и её можно будет обрезать, в правильных руках это может быть интересным стилистическим приёмом. Но вернёмся к решению, от которого у нас остаётся не так много.

\[ \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}C''_{s_{x}s_{y}}(t)\delta_{s_{x}k_{x}}\delta_{s_{y}k_{y}} = \sum_{s_x=1}^{m}\sum_{s_y=1}^{m}\lambda_{s_{x}s_{y}} C_{s_{x}s_{y}}(t)\delta_{s_{x}k_{x}}\delta_{s_{y}k_{y}} \] \[ C''_{s_{x}s_{y}}(t) = \lambda_{s_{x}s_{y}} C_{s_{x}s_{y}} \] \[ C_{s_{x}s_{y}} = A_{s_{x}s_{y}}a_{s_{x}s_{y}}^{-t} + B_{s_{x}s_{y}}a_{s_{x}s_{y}}^{t} \text{, где } a_{s_{x}s_{y}}=e^{\sqrt{\lambda_{s_{x}s_{y}}}} \] \[ \begin{cases} A_{s_{x}s_{y}}+B_{s_{x}s_{y}}=I_{1,s_{x}s_{y}} \\ A_{s_{x}s_{y}}a_{s_{x}s_{y}}^{-1}+B_{s_{x}s_{y}}a_{s_{x}s_{y}}=I_{2,s_{x}s_{y}} \end{cases} \] \[ \begin{cases} A_{s_{x}s_{y}} = \frac{ a_{s_{x}s_{y}}I_{2,s_{x}s_{y}}-a_{s_{x}s_{y}}^{2}I_{1,s_{x}s_{y}} }{ 1-a_{s_{x}s_{y}}^{2} } \\ B_{s_{x}s_{y}} = I_{1,s_{x}s_{y}}-A_{s_{x}s_{y}} \end{cases} \]

Так, ну давайте глянем, что у нас получается при разных приближениях в момент \(t=0\).

А вот при изменении t у меня возникают проблемы:

По количеству квадратов могу предположить, что на \(m=12\) случается оверфлоу и мы видим только 13 приближение и выше. Учитывая, что эта штука возникает всегда после 11 приближения, и мы апроксимируем кирпичи перьями то, возможно, это случается из-за феномена Гиббса. В общем придётся смотреть на малое приближение.

Так себе результат, мы получили виньетку+размытие+fade out/in, которые при этом дорогие в вычислениях. Я разочарован, особенно учитывая, что мне пришлось мозгу́ напрячь.

Считаем вслепую

Не хотелось мне применять этот метод, но

\[ \frac{\partial^{2}u}{\partial t^{2}} \approx \frac{(u_{n+1}-u_{n})-(u_{n}-u_{n-1})}{\Delta t^{2}} = \frac{u_{n+1}+u_{n-1}-2u_{n}}{\Delta t^{2}} \]

Да, мы ступаем в мир полностью численных методов, всё аналитическое остановится на выражении \(u_{n+1}\). Мы знаем начальное состояние, значит, можем вычислить следующее через какой-то малый промежуток времени \(\Delta t\).

\[ u_{n+1} = \Delta t^{2}\Delta u_{n} + 2u_{n} - u_{n-1} \]

Ладно, чуть-чуть наврал, подумать придётся всё-таки, сейчас, если мы просто подставим наше первое изображение как \(u_{0}\), то уйдём непонятно куда, а нам бы хотелось сделать \(N\) шагов и прийти ко второму изображению. И самая главная проблема: что такое \(u_{-1}\)? В целом это может быть решением нашего первого вопроса. По сути \(u_{-1}\) задаёт скорость изменения в начальный момент времени, то есть мы можем подобрать такое значение, чтобы дать толчок функции в нужную сторону. Как аналитически найти \(u_{-1}\) я не придумал, поэтому обратимся к задачам на оптимизацию.

Мне эта проблема напомнила обучение нейросетей: у нас есть несколько “слоёв”, через которые мы прогоняем входные данные и получаем выходные. Один из методов обучения, когда у нас есть способ автоматически оценить результат, это обратное распространение ошибки; более общий случай называется градиентным спуском. Мы задаём функцию ошибки, зависящую от входных данных и берём градиент, который показывает направление наибольшего увеличения функции, соответсвенно, если мы пойдём в другую сторону, то максимально уменьшим ошибку. Для нас всё просто, смотрим на то как сильно мы промахнулись с итоговым значением.

\[ E = u_{N}-I_{2} \]

Естественным образом мы не можем просто добавить эту поправку к \(u_{-1}\), поскольку перед тем как получить результат наши значения проходят кучу преобразований, поэтому прогоним ошибку через наше уравнение в обратном направлении.

\[ E_{n-1} = \Delta t^{2}\Delta E_{n} + 2E_{n} - E_{n+1} \]

А чо такое \(E_{N+1}\)… Ладно, тут паниковать не нужно, всё станет яснее, если мы вернёмся к непрерывному случаю.

\[ E(x,y,1)=u(x,y,1)-I_{2} \]

То есть ошибка это какая-то функция от времени и нам нужно найти E(x,y,0). Пока \(E\) уменьшается с приближением к правильному ответу и увеличивается с отдалением, это валидная функция ошибки, поэтому давайте добавим условие, которое нам поможет и никак не повлияет на поведение \(E\) в конечный момент времени.

\[ E_{t}|_{t=0}=0 \]

И, применяя секретную технику, мы получим:

\[ \frac{E_{N-1}-E_{N+1}}{2\Delta t}=0 \Leftrightarrow E_{N-1}=E_{N+1} \]

\[ E_{N+1} = \Delta t^{2}\Delta E_{N} + 2E_{N} - E_{N+1} \]

\[ E_{N+1} = \frac{1}{2}\Delta t^{2}\Delta E_{N} + E_{N} \]

И вот мы получили \(E_{0}\), которое является ошибкой для значения производной в начальный момент времени.

\[ u_{t}|_{t=0}-E_{0} \approx \frac{u_{1}-u_{-1}}{2\Delta t} \]

\[ u_{1} = 2\Delta t(u_{t}|_{t=0}-E_{0})+u_{-1} \]

\[ 2\Delta t(u_{t}|_{t=0}-E_{0})+u_{-1} = \Delta t^{2}\Delta u_{0} + 2u_{0} - u_{-1} \]

\[ u_{-1} = \frac{1}{2}\Delta t^{2}\Delta u_{0} + u_{0} - \Delta t(u_{t}|_{t=0}-E_{0}) \]

Здесь под \(u_{t}|_{t=0}\) подразумевается старое значение производной, которое мы сохраняем во время прямого прохода. И вот что мы получаем:

Ну, прямо как то, что нам показало решение методом Галёркина, значения при первой экспоненте с ростом \(t\) затухают, а при второй растут. Однако тут появились белые артефакты, скорее всего из-за аппроксимации оператора Лапласа: это же сумма вторых производных, то есть там где граница двух цветов будет скачок функции. Можно заметить, что у всех объектов появилась этакая обводка. Как раз на стыках разных вещей наибольшая вероятность встретить резкое изменение цвета.

Вроде и нельзя назвать такой результат успехом, потому что второе изображение выглядит отвратительно, а с другой стороны мы создали аппарат, который построил маршрут из одного места в другое внутри выдуманного нами пространства, хоть и не прямо к месту назначения, но к очень близкому. Вот, кстати, финальный кадр после каждой поправки.

Другие уравнения

Вот ещё парочка уравнений с интересными эффектами. Первым на очереди стоит уравнение теплопроводности, оно усиливает перепады значений, выделяя границы и повышая чёткость изображения.

\[ u_{t} = \Delta u \]

Обратным действием обладает уравнение анизотропной диффузии, которое собственно пришло из области обработки изображений, используется оно для уменьшения количества деталей. Важным параметром в нём является \(k\), который определяет чувствительность к границам. Я в уравнении заменил первую производную по времени на вторую, так оно лучше считалось и сохранялся эффект размытия.

\[ u_{tt} = \text{div} \left( \exp \left( -\frac{||\nabla u||^{2}}{k^{2}} \right) \nabla u \right) \]

Если выкрутить k слишком сильно, то можно будет заметить, как от границ расходятся волны.

В этом уравнении экспонента уменьшает векторы, если они большие и увеличивает если они маленькие, давайте тогда посмотрим, что будет, если нормализовать векторное поле.

\[ u_{tt} = \text{div} \left( \frac{\nabla u}{|\nabla u|} \right) \]

Оно достаточно быстро уничтожает изображение, но если остановиться на первых кадрах, то будут видны плавные переходы между похожими цветами. Анизотропная диффузия же создаёт пятна одного цвета, чем-то напоминает квантование изображения, особенно это заметно на облаках.

Итоги

Когда в очередной раз вспоминаю, что могу мерить удава не числами, а попугаями, у меня взрывается мозг — просто ступор и радость, это ощущается чем-то магическим.

В детстве я нередко выдумывал заклинания и фантастические миры. Когда подрос увлёкся разными играми на подобие D&D, где преимущественно брал разные сорта волшебников. Есть какой-то шарм в образе человека, который знанием буквально меняет мир вокруг себя.

И вот сейчас я сижу на лекциях и слушаю теорию, как интересную сказку. На семинарах решаю выдуманные кем-то задачки, вырисовывая какие-то символы. А потом дома, решив проверить всё, вижу как эти закорючки описывают мир вокруг меня, как они дают ответы для получения нужных результатов. Выходит, всё это правда, и я познаю то, что способно определять мир вокруг. Получается, сказка оказалась реальностью.